There has been a fair amount of confusion about how surprise is conducted in AD&D 1e. I don’t know why because right there on page 61 of the DMG it says:

Surprise is basically self-explanatory. Well then no more need be said. For something so self-explanatory, there is a lot of confusion. I’ll say a little more.

In its simplest form, each side meeting one another rolls a die (usually a d6). Some defined number sets the odds and length of one’s (the roller’s) surprise (usually a 1 or 2 on a d6). The value rolled being the length of time in segments (10 seconds each) that that party is surprised.

If both sides are surprised, then some surprise might be cancelled or offset by the other party’s own surprise. For example, Side A rolls a 2 and Side B rolls a 1. In this case, both sides are surprised, but the effect of Side A’s surprise is reduced to 1 segment because Side B is also surprised for 1 segment. In essence, Side B gawks at Side A for a segment, but regains their composure and then can act for one segment before the still gawking Side A can react.

If only one side is surprised, then the length of the surprise is the value in segments that the surprised party rolled.

The DMG p62 lays out the permutations. However, there is an error in the example. In the case of one side rolling a 1 and the other a 2, it has the listed surprised party reversed. In the end, for this example, if one is consistent, it doesn’t matter. But, in other cases, it really could matter.

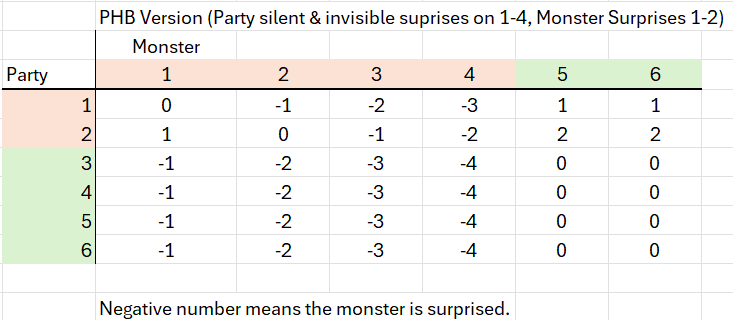
The PHB p.103 has another example where this distinction matters.

In the PHB example, the party has an advantage, they are moving silently and are also invisible. This means the monster is surprised if it rolls a 1 -4, while the party itself is only surprised on the usual 1-2 roll. In this case the permutations in the PHB show it correctly, with the side that rolls more surprise being the surprised party.

Yet, the PHB example also contains an error — just not as obvious one at first glance. It leaves out what happens if the party rolls a 2 and the monster rolls a 3 or 4. In that case, the monster is surprised.

Below, I have laid out the DMG version. Negative values indicate segments the monster is surprised, positive values segments when the Party is surprised. The rolls marked orange are surprised segments, green unsurprised segments.

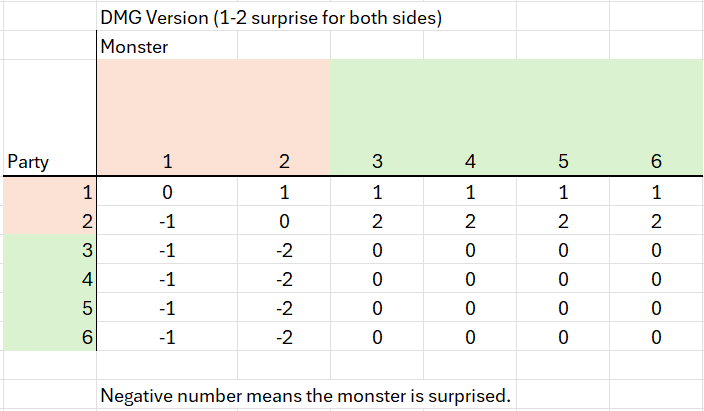
Next is the PHB example. Clearly, being both silent and invisible is a big advantage. The party has only a 14% chance of being surprised while the monster has a 58% chance of being surprised. Whereas, under normal circumstances, both sides have a 25% chance of being caught with their pants down.

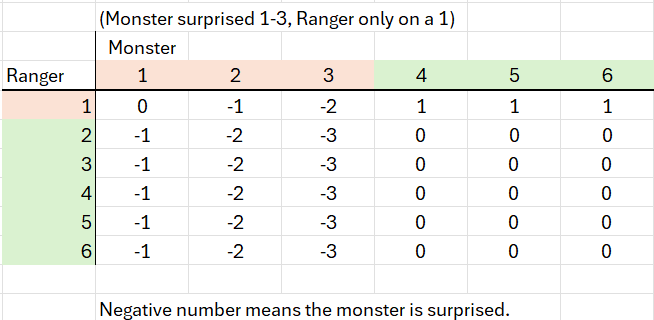
Another common scenario is the case of the Ranger. PHB p.24 details the Ranger’s surprise ability.

The Ranger not only has better odds to surprise, he also shifts the odds away from being surprised himself. The percentages shown in the PHB are a little misleading. Sure, 1-3 on a d6 represents 50%, because the surprise rule offsets mutual surprise, the odds get a lot better. The Ranger suffers the effect of being surprised only three times out of thirty-six, or 8.3 percent. Whereas, the Rangers opponents, suffer the consequences 47.2 percent of the time. It’s good to have a ranger on one’s side.

This does raise a question. What about Ranger v. Ranger? I don’t know the solution here, so I’ll present two possibilities. It says the Ranger is only surprised on a 1 in 6. It also says, a Rangers opponents are surprised on a 3 in 6. It’s paradox. So, I’ll show both 1 in 6 and both 3 in 6.

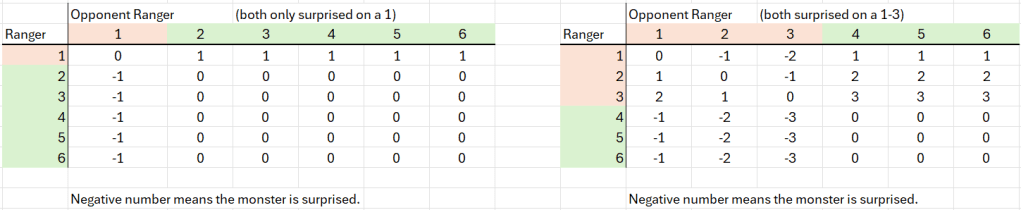
In one case, each ranger has a 14% chance of surprising the other. In the other case, a 33% chance of surprising on another. I lean toward the lower odds version, rangers would know when another is about. Another way to look at it is that the PHB says the Ranger is only surprised 50%, so half normal. Normal for a ranger being 1-3, so half being 1-1.5 which rounds to 1-2. If so, that’s the regular 1-2 that’s the base normal surprise roll. Could it be that rangers cancel each other out? Kind of makes sense to me.

There is also Dexterity to consider. If a character has a dexterity modifier (either a bonus or a penalty), if they are surprised, that bonus or penalty is added to the number of segments of surprise. A character with a Dexterity of 18 with a +3 Reaction Adjustment, who gets surprised for two segments, negates the two segments of surprise. Note though that even though the +3 is greater than 2, dexterity can never create a surprise situation, so the additional modifier is lost. An unfortunate character with a dexterity of 3, with a -3 penalty, would though increase the two segments of surprise to five segments.

Page 102 of the PHB also notes that some creatures may be especially hard to surprise, and use other dice than a d6.

A cursory review of the Monster Manual identifies no monsters explicitly stated to use a different die. There are some monsters that are surprised only on a 1, others with improved odds to surprise (1-3, or 1-4, etc.), and some that are never surprised. But, none that I found that use a different die. Nor, am I sure exactly how these features are to be addressed when facing a Ranger. For example, the Elf section of the Monster Manual says elfs surprise others on a 1-4. The Ranger description says they are only surprised on a 1, rather than the normal 1-2. So, half the elf ability back to the normal 1-2?

So, there you have it. It’s not fully explained. But, this should go a long way to adjudicating most situations.

Addendum:

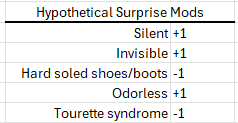
Factors that influence surprise. Uh. Hmm. It’s a judgment call. That PHB example implies that being both silent and invisible increases one’s chance of surprising something. One might also assume that silence adds a +1 and then invisibility adds another +1 — these then add to the normal 1-2 to create that surprise of 1-4 in the example. However, I see nothing in either the PHB or the DMG that says that explicitly. Each DM will need to adjudicate the exact situation as to what these effects might have on surprise. Even looking into the OD&D books does not elucidate the effect of silence or invisibility on surprise. Yet, I think each adding a +1 is a good rule of thumb.

Addendum 2: Monks

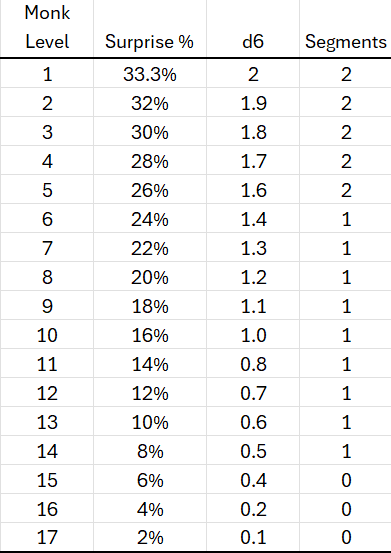
I totally forgot about Monk’s surprise ability.

So, argh, percentages now? How to integrate that into the d6 approach. Table below translates percentage to d6 and segment values. So, I’d roll the Monk’s surprise using percentile dice and then translate it to Segment values. Also, I didn’t find any discussion of it, but I would allow Monks to roll their surprise separate from group initiative. Unlike Rangers, which can use their initiative for the group, I don’t see Monk’s being able to do that.

Addendum 3