Here’s a short one with no real conclusion. This really is just a place to memorialize where I am in thinking about this subject. And, to inspire anyone who also might be interested in the topic.

War games often have game mechanisms for rolling dice to determine whether an attack is successful or not. But how are these odds determined? The game rules rarely discuss this. Sometimes there might be a reference given to some set of statistics or another, but this is unusual. Most of the time, how the odds were determined is a black box. This is true for Dungeons and Dragons.

The original Dungeons and Dragons (OD&D) Alternative Combat System has Levels 1-3 needing a ten to hit armor class nine, then adding one for each drop in armor class thereafter. This has remained, more or less, similar in all versions of Dungeons and Dragons.

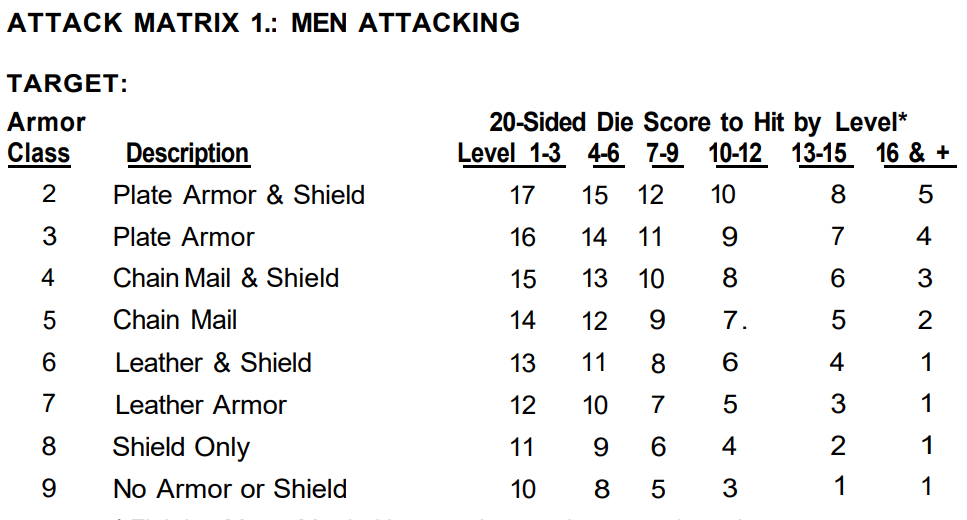
Advanced Dungeons and Dragons (AD&D) expanded the scale downward a bit. There is a level zero which needs a twelve to hit AC 9. Plus, they added a variety of attack tables for different classes. The 10 to hit AC9 doesn’t appear in the fighter attack table, but the OD&D value would be somewhere between second and third level. But AC9 in OD&D is really AC10 in AD&D. In OD&D the lowest level (1st) has a 55 percent chance to hit an unarmored opponent, this is the same for a first level character in AD&D to hit AC10 (unarmored). So, really, it’s the same system with the armor class scale expanded and level 0 added below level 1.

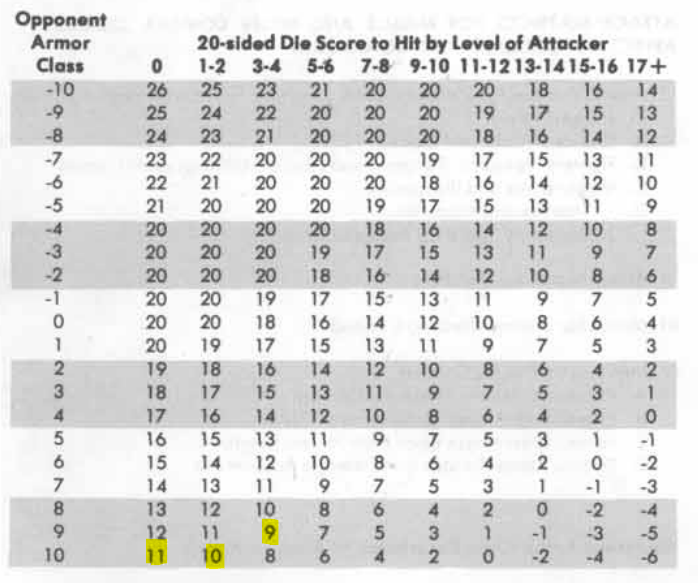
The question for me is why these chosen odds? We know the length of a combat round in D&D is 1-minute. And, we know from the AD&D Dungeon Masters Guide (DMG) that the single to-hit roll is a statistical representation of many attack and defense activities that occur within that one minute. We know it is accurate that a lot can go one within one minute. YouTube is full of examples. So, the combined roll to hit and the roll of damage dice does not reflect a single attempt to strike. Nor, does the damage a weapon causes represent the effect of a single strike. There may be several successful strikes in a round, all of which do some injury, that in aggregate equal the damage rolled from a successful “to-hit” roll. Conversely, we know that within a round a character may make many strikes that fail to do injury that nonetheless in game terms cause hit-points of “damage”. This damage may be represented as exhaustion, sprains, sweat in one’s eyes, or whatever “hit-points” represents that prevents one from taking that final killing blow.

So, how did they determine that within a one-minute round of fighting there is a 55 percent chance of being affected? I don’t know. So, I asked the bros whether they knew. They did not. But, I did get one suggestion. Stephen Smith suggested that I take a look at Tony Bath’s Peltast and Pila. He even sent me a helpful copy of the chart he was referring to. And, sure enough there do seem to be some similarities there.

In addition to the naming convention using “and” (Peltast & Pila, Dungeons & Dragons), the armor list uses a convention familiar to Dungeons and Dragons players, the armor tables work from unarmored to more heavily armored and combine shields + weak armor = a stronger armor. For example in Bath Leather + Shield is equivalent to half armor. Then half armor + shield is equivalent to a Chain Shirt. Similarly, in AD&D Leather + Shield equals Studded Leather, and Studded Leather + Shield equals Scale Mail.

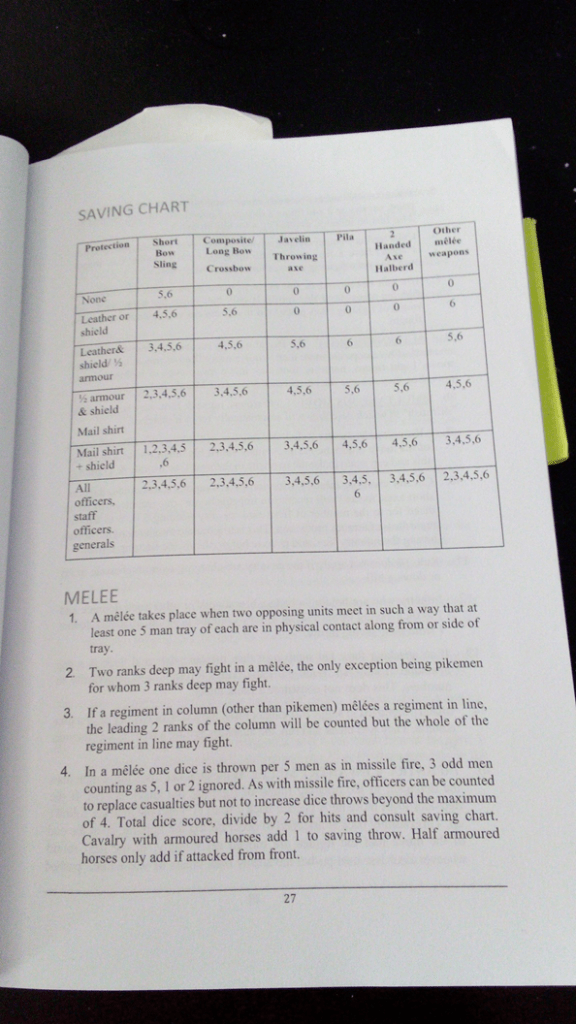
But the combat resolution in Bath is totally different from the method in D&D. One cross-references the means of attack with the armor type and then a d6 is rolled and the odds of causing a casualty are listed for each permutation. There is no to-hit roll and then a damage roll, for Bath it’s all one step.

Well, not exactly. For Bath, this is a mass combat system. In simple terms one rolls one die for every five men attacking, sums the dice up and then divides the result by two to determine casualties, then each casualty gets a saving throw using the numbers on the table. For normal melee weapons, unarmored units get no saving throw, but the better the armor, the better the saving throw. The upshot then is that for every unarmored figure, that divide by two means fifty percent odds of survival. This may not be strictly true in all cases but, it’s something like that.

So, I then went and calculated the odds of surviving an attack using Bath’s system. Then I did the same for AD&D. Now, I needed to make some assumptions. The first being that for low level (or zero or first level) characters, that the average damage roll will kill such a character. A typical 0-level mercenary in AD&D has 4-7 hp with an average of 5.5 hp. The average spear might do 3.5 hp damage, and even a broadsword 5 hp average damage. So, maybe this isn’t a great assumption for AD&D. But we must remember that in OD&D the hit dice are based on Chainmail and are d6s, so then a common soldier would have 3.5 average hp. In any case, I went with the assumption that an average D&D hit kills.

So, when comparing the Bath odds of survival with the D&D odds of survival, I came up with this.

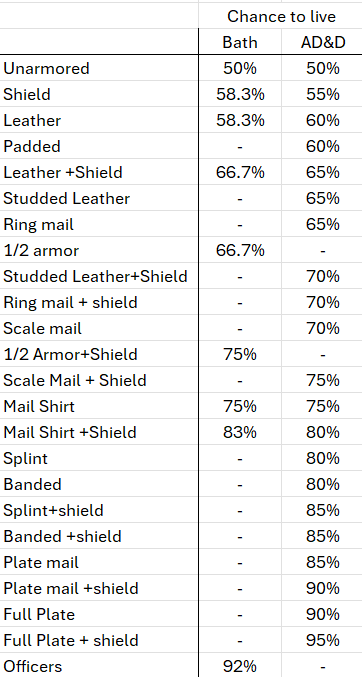
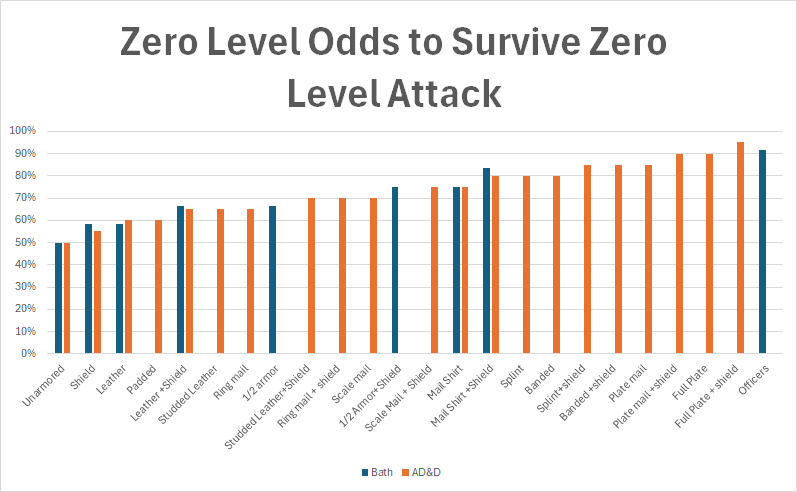
While, AD&D adds lots of different armor types and Bath has some armor not present in AD&D, there are a few things to note. The first and most important is that for unarmored and for chain mail (mail shirt) the odds of survival came out exactly the same. The second observation is that for the other armors in common between the two systems, the odds came out, if not exact, then very similar. These could be errors on my part or just the sort of compromises in granularity between using six-sided to other kinds of dice. I’m not saying this is a smoking gun, but I would not be surprised if the Alternative Combat System (and possibly the Chainmail system) were based on the odds generated by the Bath system. Or, at least, both Bath and Gygax/Arneson, made very similar base assumptions. Because if guess how effective chain mail is, why would two guesses be exactly the same?

But why that assumption? I do not know. It could be that they both were referring to some earlier source? It does kind of stand to reason that at its most simplistic, if two people are fighting, one must win and the other must lose. So fifty percent chance to be modified by other factors such as armor. It does seem to be another clear indication of how mass combat rules were used to determine individual combat success in OD&D. There is more digging into historical sources to be done here. But this seems like a step in the right direction, and thanks to Stephen for pointing me in it. I look forward to seeing what more we might find.